Análisis e comparativas
WORK IN PROGRESS
Si, tod@s o sabemos. As computadoras funcionan con ceros e uns. Sistema binario. Un feixe deles. Ok, compro, pero… de verdade isto que estou a escribir no meu portátil, que vai subir a internet e que ti estarás a ler son ceros e uns? CEROS E UNS? Que clase de maxia negra é esa? Este artigo tentará recopilar experimentos sinxelos que, agardo, me permitirán comprender un pouco mellor este proceso e, así, ser capaz de explicarlle mellor aos meus alumnos de ESO como é que, cando consultan o seu Instagram, está a ollar para unha sucesión inabarcable de interruptores que se acenden e se apagan. NON imos crear un curso completo de lóxica e electrónica dixital, unicamente imos montar algúns dispositivos físicos que demostran algúns conceptos de ciencia computacional. Como resultado final, xuntando estes dispositivos, construiremos un ADCNand (Absurdo Dispositivo Computacional baseado en portas NAND).
Bueno, só foi unha vez… e eu era novo e inconsciente, xa paguei a miña débeda coa sociedade! Ah, non era iso o que tiña que contar aquí? Vale, entón nos centraremos no tema. Un bo punto de partida é verse a lista de vídeos de code.org titulada How computers work?. Mália que sae Bill Gates, que representa unhas cantas cousas que non me gustan do mundo da tecnoloxía, eses vídeos dannos un marco de referencia no que comezar a traballar. Alo menos, temos un comezo, a estrutura dunha computadora!
En galego, “Entra, Almacénase, Procésase e Sae”. Ese é o esquelete conceptual de calquera dispositivo ao que poidamos chamar máquina de computación. Ordenadores, móbiles, smartwatches, calculadoras e iTrebellos varios, todos respostan a este esquema. Os proxectos que imos ir desenvolvendo a continuación tentarán demostrar como funcións que consideramos intelectuais, propias de algo que denominamos “intelixencia humana”, poden ser implementadas con sinxelos circuítos eléctricos.
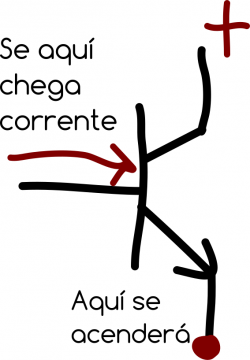
Igual xa o escoitaches por aí. TODO son transistores. Existen e existiron outros xeitos de facer computación, pero, de momento, os transistores son as unidades básicas dunha computadora. E… como son eses todopoderosos dispositivos? que clase de feitizos son capaces de crear para traerme a casa os vídeos de “El Rubius OMG”? Pois poden… redoble de tambores… luces fóra… cambiar de estado eléctrico cando reciben unha corrente! Tachaaaaaaaaaaaaaaaaaaaaaaaan! Si, aínda que non o pareza, iso é MOITO! Para que che quede un pouco máis claro, deixámosche un debuxo que o explica todo (mal).
Se queres profundizar no funcionamento dos transistores, tes bo material na páxina de María Loureiro.
Antes xa de que se inventaran as computadoras, os transistores ou o buscaminas, houbo un home, George Boole que se dedicou a estudar as matemáticas desde unha perspectiva binaria, creando o que hoxe se coñece como álxebra de Boole. Este álxebra propón que podemos descompoñer operacións matemáticas e de lóxica filosófica complexas en operacións sinxelas (AND, OR, NOT…) aplicadas a estados binarios. Non imos entrar moi a fondo nos postulados de George Boole, xa que podes profundizar pola túa conta lendo o seu tratado, de atractivo título, An Investigation of the Laws of Thought on Which are Founded the Mathematical Theories of Logic and Probabilities. Seguro que, antes de telo rematado, xa te decatarás de que, se cun transistor podemos conseguir dous estados (chámalle aceso e apagado, on/off, alto e baixo, true ou false ou cero e un), poderemos empregar a elećtrónica para desenvolver as teorías booleanas e crear un mundo no que complexos procesos intelectuais se descompoñen en interaccións binarias.
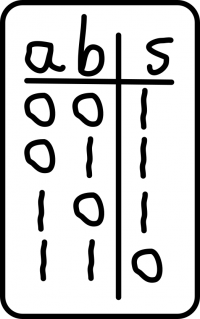
En electrónica existen uns dispositivos, chamados portas lóxicas, que poden recrear operacións de álxebra booleana con electricidade. Esas portas lóxicas poden ser construídas con transistores, e nós imos facer o noso primeiro pequeno proxecto montando unha delas, a porta NAND. A porta NAND é un dispositivo que funciona dacordo coa táboa de verdade da imaxe, o cal quere dicir que nos dará un 1 na saída sempre e cando as súas dúas entradas non sexan, á súa vez, un 1.
Este é o símbolo dunha porta NAND
Titorial orixinal en instructables
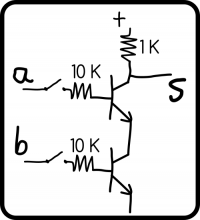
Empregando notación electrónica, o que imos montar é isto:
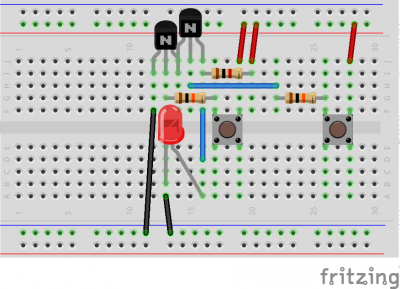
Máis graficamente, poderiamos facelo como nesta outra imaxe. (Estes esquemas son aclaratorios pero non implican que sexa a forma optimizada de montar os circuitos).
E, sendo xa moi xenerosos, tamén vos poñemos unha fotografía.
Se alimentas o circuito cuns 6 voltios, poderás ver como o LED, que indica a saída, estará aceso sempre e cando non premamos os dous botóns (entradas “a” e “b”) ao mesmo tempo, cumplindo coa táboa de verdade dunha porta NAND. Seguro que estás a pensar que isto foi moito traballo para conseguir algo tan sinxelo, pero pensa que, só cuns 1.000.000.000 de montaxes coma este, interconectados entre si, poderías construír un procesador moderno!
Unha vez sabemos montar unha porta NAND imos empregar 27 delas para construír un circuito capaz de facer… sumas! Pero non unha suma calquera, senón sumas até o 14! (aplausos e exclamacións de admiración)
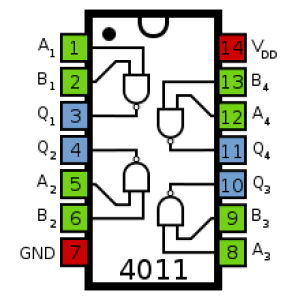
Se estás a pensar en saír deste artigo e non voltar xamáis a abrilo, que saibas que existen uns circuitos integrados moi cuquis que xa traen as portas montadas e nós só temos que usar as súas entradas e saídas, co que aforraremos moito traballo. Estes integrados teñen uns nomes tan suxerentes como CD4011 e 74HC00. Sen ningunha dúbida, imos empregar o primeiro. Principalmente, porque tiña dez na miña caixa de ferramentas e non sabía que facer con eles. Con 74HC00 se podería facer perfectamente, só habería que cambiar algún cableado tendo en conta o seu pinout.
Estes son os pines dun CD4011, podes ver que hai un pin de positivo, outro de masa e, o resto, son entradas e saídas de portas NAND.
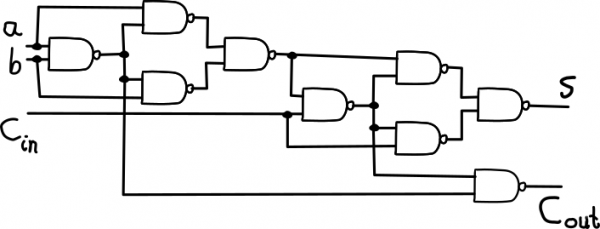
E este é o esquema de conexión dun sumador completo ou “full adder”, que é un circuito que pode coller dous bits e un acarreo de entrada e sumalos para darnos un bit de resultado e un acarreo de saída.
Montando o circuito da imaxe unha vez, podemos sumar dous números binarios dunha cifra (un bit), pero se o repetimos e encadeamos os acarreos de saída (Cout) cos de entrada (Cin), poderemos sumar tantos bits como repeticións do circuito fagamos! Nós imos facer un sumador de números de tres bits, porque nos colle nunha breadboard de 800 puntos e cremos que sumar números até o 14 xa é unha demostración suficiente do poder das NAND. Poño un esquema do sumador, non sei se aclarará moito, pero despois do tempo que me levou facelo, terei que colgalo nalgún sitio…
Se cadra o ves mellor descargando o .svg orixinal.
Co sumador xa temos un exemplo moi básico (outros dirían ridículamente básico) de procesado de datos, pero eses datos os temos que introducir a man dun xeito moi primitivo, colocando os cables de entrada na liña de positivo ou de masa. Fáltanos un proceso esencial, do que xa falamos, no esquema dunha computadora, a memoria de datos. Precisamos algún circuito que poidamos poñer nun estado determinado e que sexa capaz de manter ese estado, iso ímolo conseguir empregando unicamente, como non… portas NAND!
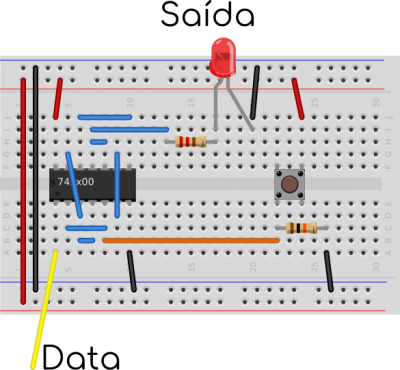
O circuito que imos montar chámase fecho ou, en inglés e máis comunmente atopado, latch, e require catro NANDs para almacenar un bit de memoria. O seu esquema é o seguinte:
O terminal Enable nos permitirá controlar cando se almacena ou non un bit, se enable está en negativo, non respostará aos cambios de estado de data. Se está en positivo, a saída será igual ao estado de data. Deste xeito, se queremos almacenar un 1, teremos que poñer enable en modo de escritura, é dicir, conectalo a positivo. Logo teremos que conectar data a positivo, para que “entre” un 1, e logo desactivar o enable poñéndoo a negativo, para que os posibles cambios en data non alteren o estado do bit que acabamos de almacenar. O bit gardado deste xeito se mostrará na saída, e no outro terminal teremos o inverso (non o imos empregar) que é o que representa esa raia por riba de “saída”. Esta vez ímolo montar cun 74HC00, porque se me acabaron os CD4011, que é un motivo técnico de relevancia indiscutible.
Se queres ter máis bits, que é o que faremos máis adiante, non tes máis que replicar este mesmo esquema. Lembra que podes encadear todos os enables ao mesmo pulsador.
Pode ser que penses que isto non é moita cousa… ao final non é máis que o que se podería facer subindo ou baixando un interruptor!! A grande diferencia está na velocidade á que se pode subir ou baixar ese interruptor, ao cambiar o estado dos nosos bits empregando pulsos eléctricos movémonos a velocidades inalcanzables para calquera ser humano ou dispositivo mecánico!
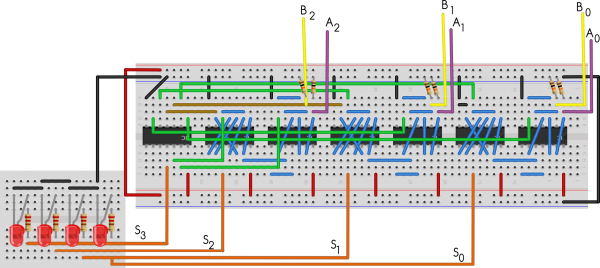
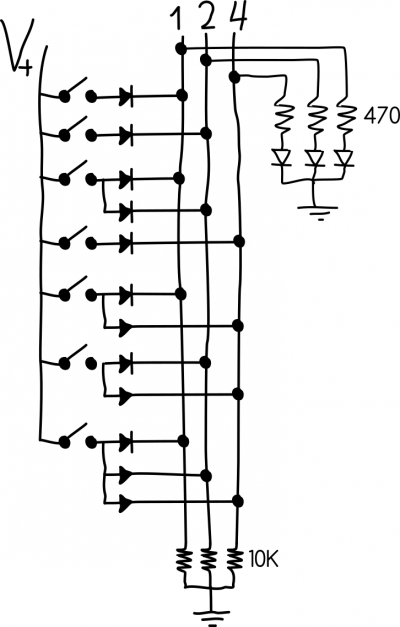
Xa temos un circuíto que almacena números e un circuíto que pode sumar estes números. Agora imos ver como podemos transformar, dun xeito un tanto rudimentario, un número do sistema ao que estamos acostumados, o decimal, ao sistema no que traballan as computadoras e os nosos dispositivos, o binario. Ímonos basear nesta montaxe, pero nada máis faremos un teclado até o sete, seguindo o seguinte esquema simplificado.
Unha das posibles montaxes sería a da figura:
Se te fixas no esquema, non é máis que asignar unha saída para cada bit do número (no noso caso, tres) e conectar os pulsadores dos números decimais coas saídas que o compoñen en binario. Por exemplo, se prememos no botón número 5, conectará a positivo as saídas do primeiro (valor 1) e terceiro bit (valor 4), co cal teremos o número binario equivalente 101. A estas saídas, logo poderemos conectar as nosas memorias para non ter que andar movendo cables. Os díodos son nada máis para illar os circuítos de cada pulsador dos demais.
Por fin!!
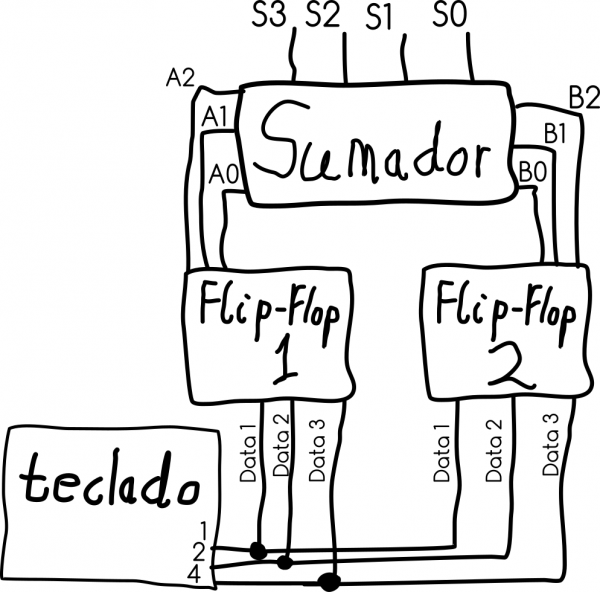
Xa sabemos facer os bloques precisos para o noso Absurdo Dispositivo Computacional con portas NAND! Agora nada máis teremos que unir todos eles para construír este summum da tecnoloxía absurda, que será capaz de memorizar nin máis nin menos que dous números binarios de tres bits cada un, e sumalos entre si! Acompáñasme? Zarpamos! (cursilería estilística sobreedulcorada adicada a justificaturespuesta)
Pois se chegaches até aquí, pouco máis que esta imaxe te fará falla…
Se queres velo funcionar, de momento tes que esperar un chisco… teño que peinarlle un pouco os cables á miña montaxe e, en canto estea ben arregladiña, fago vídeo.
Este cacharro levoume moito máis tempo e blasfemias do que contaba. Pensando na lóxica dixital, tíñame imaxinado que todo sería sinxelo, entrada positiva, saída negativa e así… pero non é tan doado. Ou si… Comecei a montaxe con compoñentes que tiña por aí ciscados, resistencias de distinto valor, ledes con consumos diferentes, diodos recuperados de outros proxectos… MAL! Despois de dar moitas voltas, cambiei todas as resistencias por 470 ohmnios, todos os ledes iguais, os diodos novos do trinque e todo funcionou! Os consumos eléctricos son importantes para a estabilidade das portas, así que, aínda que pareza que, cando a montaxe é sinxela, todo funciona independentemente do que lle poñamos á saída e da voltaxe coa que alimentemos, mellor limitar ben a corrente de saída cunhas boas resistencias.
Si, se chegaches aquí para tirarme das orellas, contén os teus impulsos! Os transistores non acenden, pero é a maneira simple de explicarllo ao meu alumnado quinceañeiro. Para ser rigorosos, debera profundizar un anaco máis e poñer un circuitiño cunha resistencia pull-algo, explicar como en ausencia de corrente a resistencia funciona como un cable… pero a explicación incorrecta nos pode servir de momento para entender este artigo.
Despois de escribir o artigo, aprendín que, ao que eu lle chamaba Flip-Flop, en realidade sería máis acertado chamarlle “Latch” ou, permitíndome exercer de tradutor, “fecho”. O flip-flop leva unha pouca circuitería extra para facer que resposte a un sinal de reloxo, mentres que o fecho non. Non é algo que estexa moi estendido, con frecuencia atoparás que se lle chama flip-flop aos fechos.
Unhas poucas cousas que me inspiraron ou que copiei, grazas a todos por compartir:
Moitos ceros e uns para todas e todos, vémonos no seguinte ciclo de reloxo!
